This is a guest post by Time Manager collaborator and Python expert, Ariadni-Karolina Alexiou.

Today we’re going to look at how to visualize the error bounds of a GPS trace in time. The goal is to do an in-depth visual exploration using QGIS and Time Manager in order to learn more about the data we have.

The Data

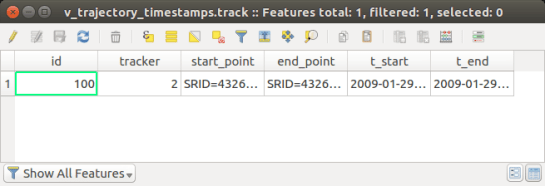
We have a file that contains GPS locations of an object in time, which has been created by a GPS tracker. The tracker also keeps track of the error covariance matrix for each point in time, that is, what confidence it has in the measurements it gives. Here is what the file looks like:

Error Covariance Matrix

What are those sd* fields? According to the manual: The estimated standard deviations of the solution assuming a priori error model and error parameters by the positioning options. What it basically means is that the real GPS location will be located no further than three standard deviations across north and east from the measured location, most of (99.7%) the time. A way to represent this visually is to create an ellipse that maps this area of where the real location can be.

An ellipse can be uniquely defined from the lengths of the segments a and b and its rotation angle. For more details on how to get those ellipse parameters from the covariance matrix, please see the footnote.

Ground truth data

We also happen to have a file with the actual locations (also in longitudes and latitudes) of the object for the same time frame as the GPS (also in seconds), provided through another tracking method which is more accurate in this case.

This is because, the object was me running on a rooftop in Zürich wearing several tracking devices (not just GPS), and I knew exactly which floor tiles I was hitting.

The goal is to explore, visually, the relationship between the GPS data and the actual locations in time. I hope to get an idea of the accuracy, and what can influence it.

First look

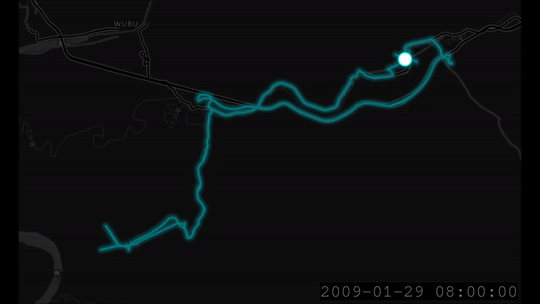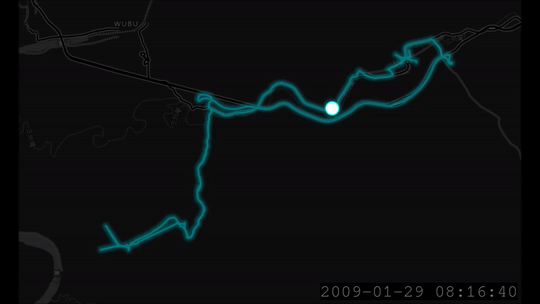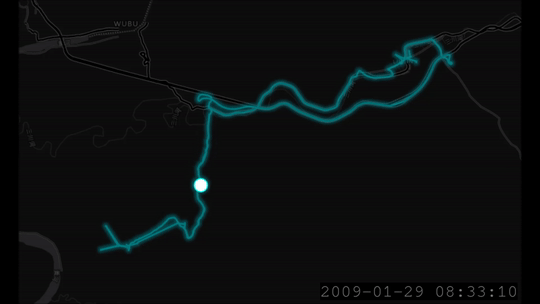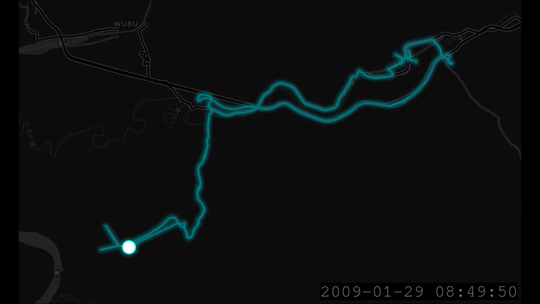
Loading the GPS data into QGIS and Time Manager, we can indeed see the GPS locations vis-a-vis the actual locations in time.

Let’s see if the actual locations that were measured independently fall inside the ellipse coverage area. To do this, we need to use the covariance data to render ellipses.

Creating the ellipses

I considered using the ellipses marker from QGIS.

It is possible to switch from Millimeter to Map Unit and edit a data defined override for symbol width, height and rotation. Symbol width would be the a parameter of the ellipse, symbol height the b parameter and rotation simply the angle. The thing is, we haven’t computed any of these values yet, we just have the error covariance values in our dataset.

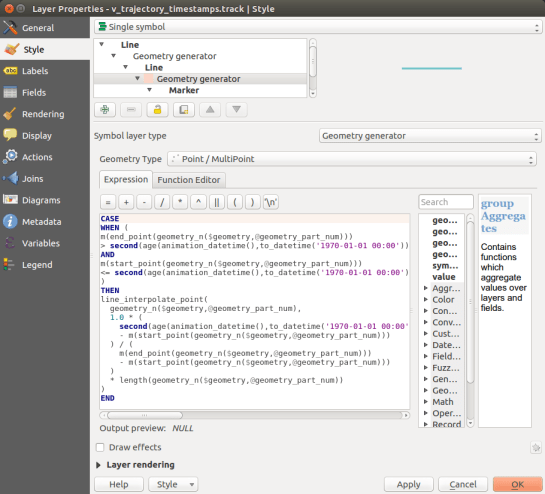
Because of the re-projections and matrix calculations inherent into extracting the a, b and angle of the error ellipse at each point in time, I decided to do this calculation offline using Python and relevant libraries, and then simply add a WKT text field with a polygon representation of the ellipse to the file I had. That way, the augmented data could be re-used outside QGIS, for example, to visualize using Leaflet or similar. I could have done a hybrid solution, where I calculated a, b and the angle offline, and then used the dynamic rendering capabilities of QGIS, as well.

I also decided to dump the csv into an sqlite database with an index on the time column, to make time range queries (which Time Manager does) run faster.

Putting it all together

The code for transforming the initial GPS data csv file into an sqlite database can be found in my github along with a small sample of the file containing the GPS data.

I created three ellipses per timestamp, to represent the three standard deviations. Opening QGIS (I used version: 2.12, Las Palmas) and going to Layer>Add Layer>Add SpatialLite Layer, we see the following dialog:

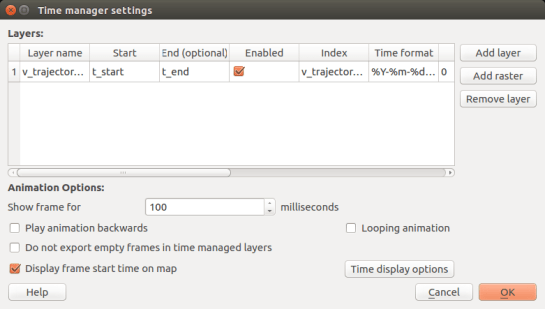
After adding the layer (say, for the second standard deviation ellipse), we can add it to Time Manager like so:

We do the process three times to add the three types of ellipses, taking care to style each ellipse differently. I used transparent fill for the second and third standard deviation ellipses.

I also added the data of my  actual positions.

Here is an exported video of the trace (at a place in time where I go forward, backwards and forward again and then stay still).

Conclusions

Looking at the relationship between the actual data and the GPS data, we can see the following:

• Although the actual position differs from the measured one, the actual position always lies within one or two standard deviations of the measured position (so, inside the purple and golden ellipses).
• The direction of movement has greater uncertainty (the ellipse is elongated across the line I am running on).
• When I am standing still, the GPS position is still moving, and unfortunately does not converge to my actual stationary position, but drifts. More research is needed regarding what happens with the GPS data when the tracker is actually still.
• The GPS position doesn’t jump erratically, which can be good, however, it seems to have trouble ‘catching up’ with the actual position. This means if we’re looking to measure velocity in particular, the GPS tracker might underestimate that.

These findings are empirical, since they are extracted from a single visualization, but we have already learned some new things. We have some new ideas for what questions to ask on a large scale in the data, what additional experiments to run in the future and what limitations we may need to be aware of.

Thanks for reading!

Footnote: Error Covariance Matrix calculations

The error covariance matrix is (according to the definitions of the sd* columns in the manual):

It is not a diagonal matrix, which means that the errors across the ‘north’ dimension and the ‘east’ dimension, are not exactly independent.

An important detail is that, while the position is given in longitudes and latitudes, the sdn, sde and sdne fields are in meters. To address this in the code, we convert the longitude and latitudes using UTM projection, so that they are also in meters (northings and eastings).

For more details on the mathematics used to plot the ellipses check out this article by Robert Eisele and the implementation of the ellipse calculations on my github.